NBLAST#

This tutorial will introduce you to NBLAST (Costa et al., 2016), a method to compare neurons based on their morphology.

What is NBLAST?#

A brief introduction (modified from Jefferis lab's website):

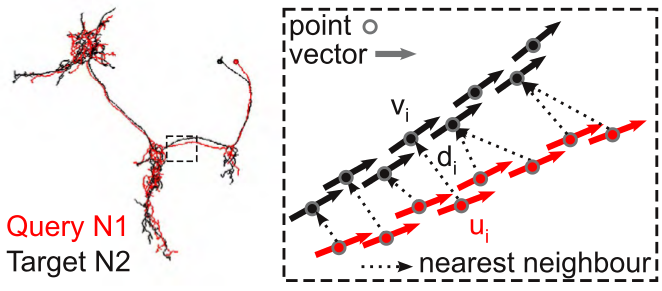
NBLAST works by decomposing neurons into point and tangent vector representations - so called "dotprops". Similarity between a given query and a given target neuron is determined by:

1. Nearest-neighbor search:

   For each point + tangent vector \(u_{i}\) of the query neuron, find the closest point + tangent vector \(v_{i}\) on the target neuron (this is a simple nearest-neighbor search using Euclidean distance).

   

2. Calculate a raw score:

   The raw score is a weighted product from the distance \(d_{i}\) between the points in each pair and the absolute dot product of the two tangent vectors \(| \vec{u_i} \cdot \vec{v_i} |\).

   The absolute dot product is used because the orientation of the tangent vectors typically has no meaning in our data representation.

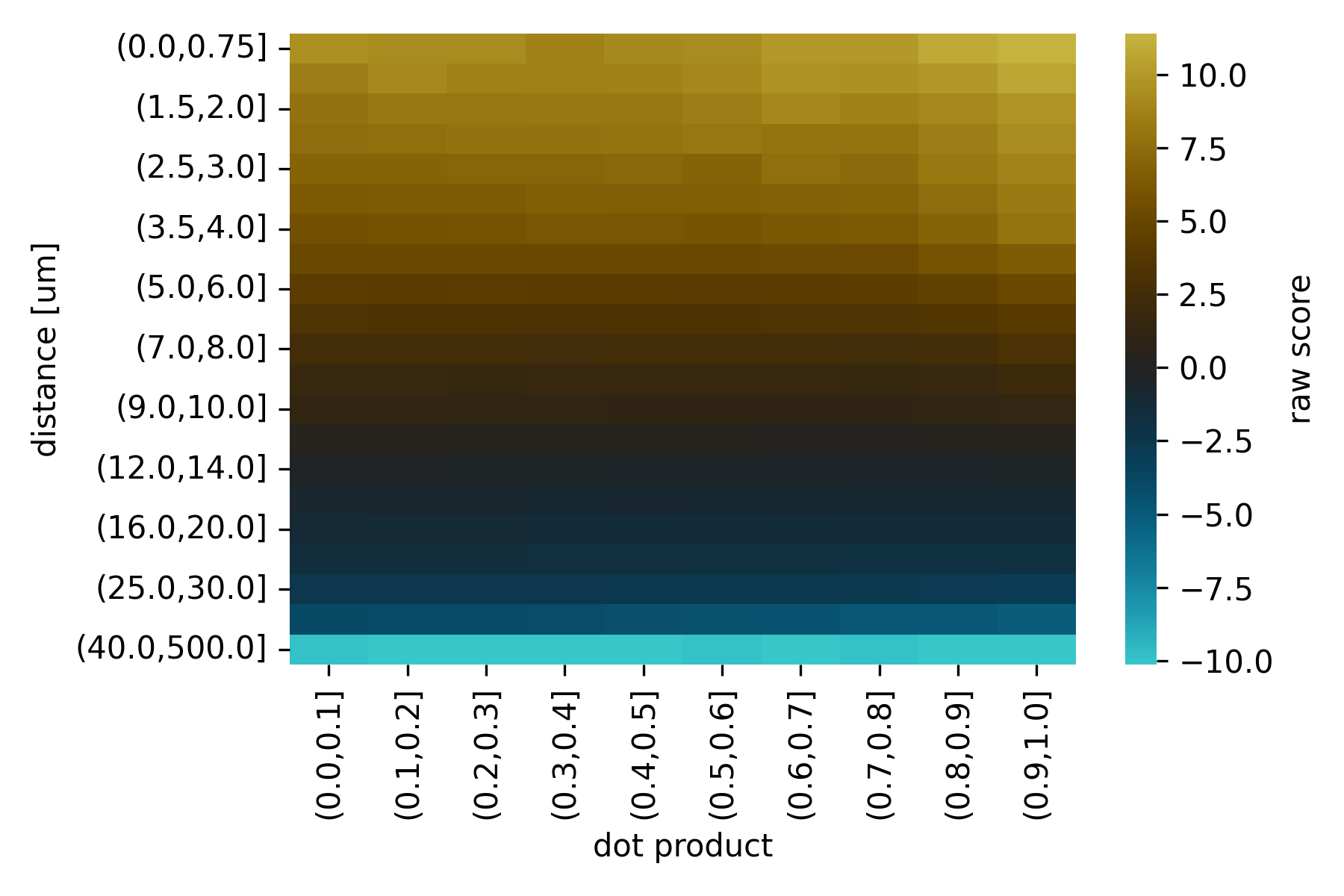
   A suitable scoring function \(f\) was determined empirically (see the NBLAST paper) and is shipped with NAVis as scoring matrices:

   

   Importantly, these matrices were created using Drosophila neurons from the FlyCircuit light-level dataset which are in microns. Consequently, you should make sure your neurons are also in micrometer units for NBLAST! If you are working on non-insect neurons you might have to play around with the scaling to improve results. Alternatively, you can also produce your own scoring function (see this tutorial).

3. Produce a per-pair score:

   This is done by simply summing up the raw scores over all point + tangent vector pairs for a given query-target neuron pair.

4. Normalize raw score

   This step is optional but highly recommended: normalizing the raw score by dividing by the raw score of a self-self comparison of the query neuron.

Putting it all together, the formula for the raw score \(S\) is:

Running NBLAST#

Broadly speaking, there are two applications for NBLAST:

1. Matching neurons neurons between two datasets
2. Clustering neurons into morphologically similar groups

Before we get our feet wet, two things to keep in mind:

• neurons should be in microns as this is what NBLAST's scoring matrices have been optimized for (see above)
• neurons should have similar sampling resolution (i.e. points per unit of cable)

OK, let's get started!

We will use the example neurons that come with NAVis. These are all of the same type, so we don't expect to find very useful clusters - good enough to demo though!

Load example neurons

import navis

nl = navis.example_neurons()

NBLAST works on dotprops - these consist of points and tangent vectors decribing the shape of a neuron and are represented by the navis.Dotprops class in NAVis. You can generate those dotprops from skeletons (i.e. TreeNeurons), meshes (i.e. MeshNeurons) (see navis.make_dotprops for details) or straight from image data (see navis.read_nrrd and navis.read_tiff) - e.g. confocal stacks.

# Convert neurons into microns (they are 8nm)
nl_um = nl / (1000 / 8)

# Generate dotprops
dps = navis.make_dotprops(nl_um, k=4, resample=False)

# Run the actual NBLAST: the first two vs the last two neurons
nbl = navis.nblast(dps[:2], dps[2:], progress=False)
nbl

Painless, wasn't it? The nbl scores dataframe has the query neurons as rows and the target neurons as columns.

Let's run an all-by-all NBLAST next:

aba = navis.nblast_allbyall(dps, progress=False)
aba

This demonstrates two things:

1. The forward and reverse scores are never exactly the same (as noted above).
2. The diagonal is always 1 because it is a self-self comparison (i.e. a perfect match) and we normalize against that.

Let's run some quick & dirty analysis just to illustrate things.

For hierarchical clustering we need the matrix to be symmetrical - which our all-by-all matrix is not. We will therefore use the mean of forward and reverse scores (you could also use e.g. the minimum or the maximum):

aba_mean = (aba + aba.T) / 2

We also need distances instead of similarities!

Invert to get distances Because our scores are normalized, we know the max similarity is 1

aba_dist = 1 - aba_mean
aba_dist

Now we can use scipy's hierarchical clustering to generate a dendrogram

from scipy.spatial.distance import squareform
from scipy.cluster.hierarchy import linkage, dendrogram, set_link_color_palette

import matplotlib.pyplot as plt
import matplotlib.colors as mcl
import seaborn as sns

set_link_color_palette([mcl.to_hex(c) for c in sns.color_palette("muted", 10)])

# To generate a linkage, we have to bring the matrix from square-form to vector-form
aba_vec = squareform(aba_dist, checks=False)

# Generate linkage
Z = linkage(aba_vec, method="ward")

# Plot a dendrogram
dn = dendrogram(Z, labels=aba_mean.columns)

ax = plt.gca()
ax.set_xticklabels(ax.get_xticklabels(), rotation=30, ha="right")

sns.despine(trim=True, bottom=True)
plt.tight_layout()

We'll leave it at that for now but just to have it mentioned: there is also a navis.nblast_smart function which tries to cut some corners and may be useful if you want to run very large NBLASTs.

These are the functions we seen so far:

• navis.nblast: classic query target NBLAST
• navis.nblast_allbyall: pairwise, all-by-all NBLAST
• navis.nblast_smart: a "smart" version of NBLAST

Another flavour: syNBLAST#

SyNBLAST is synapse-based NBLAST: instead of turning neurons into dotprops, we use their synapses to perform NBLAST (minus the vector component). This is generally faster because we can skip generating dotprops and calculating vector dotproducts. It also focusses the attention on the synapse-bearing axons and dendrites, effectively ignoring the backbone. This changes the question from "Do neurons look the same?" to "Do neurons have in- and output in the same area?". See navis.synblast for details.

Let's try the above but with syNBLAST:

# Importantly, we still want to use data in microns!
synbl = navis.synblast(nl_um, nl_um, by_type=True, progress=False)
synbl

The same as above, we can run an all-by-all synNBLAST and generate a dendrogram:

aba_vec = squareform(((synbl + synbl.T) / 2 - 1) * -1, checks=False)

Z = linkage(aba_vec, method="ward")

dn = dendrogram(Z, labels=synbl.columns)

ax = plt.gca()
ax.set_xticklabels(ax.get_xticklabels(), rotation=30, ha="right")

sns.despine(trim=True, bottom=True)
plt.tight_layout()

A real-world example#

The toy data above is not really suited to demonstrate NBLAST because these neurons are of the same type (i.e. we do not expect to see differences).

Let's try something more elaborate and pull some hemibrain neurons from neuPrint. For this you need to install the neuprint-python package (pip3 install neuprint-python), make a neuPrint account and generate/set an authentication token. Sounds complicated but is all pretty painless - see the neuPrint documentation for details. There is also a separate NAVis tutorial on neuprint here.

Once that's done we can get started by importing the neuPrint interface from NAVis:

import navis.interfaces.neuprint as neu

# Set a client
client = neu.Client("https://neuprint.janelia.org", dataset="hemibrain:v1.2.1")

Next we will fetch all olfactory projection neurons of the lateral lineage using a regex pattern.

pns = neu.fetch_skeletons(
    neu.NeuronCriteria(type=".*lPN.*", regex=True), with_synapses=True, client=client
)

# Drop neurons on the left hand side
pns = pns[[not n.name.endswith("_L") for n in pns]]

pns.head()

Generate dotprops

# These neurons are in 8x8x8nm (voxel) resolution
pns_um = pns / (1000 / 8)  # convert to microns
pns_dps = navis.make_dotprops(pns_um, k=5)
pns_dps

Run an all-by-all NBLAST and synNBLAST

pns_nbl = navis.nblast_allbyall(pns_dps, progress=False)
pns_synbl = navis.synblast(pns_um, pns_um, by_type=True, progress=False)

# Generate the linear vectors
nbl_vec = squareform(((pns_nbl + pns_nbl.T) / 2 - 1) * -1, checks=False)
synbl_vec = squareform(((pns_synbl + pns_synbl.T) / 2 - 1) * -1, checks=False)

# Generate linkages
Z_nbl = linkage(nbl_vec, method="ward", optimal_ordering=True)
Z_synbl = linkage(synbl_vec, method="ward", optimal_ordering=True)

# Plot dendrograms
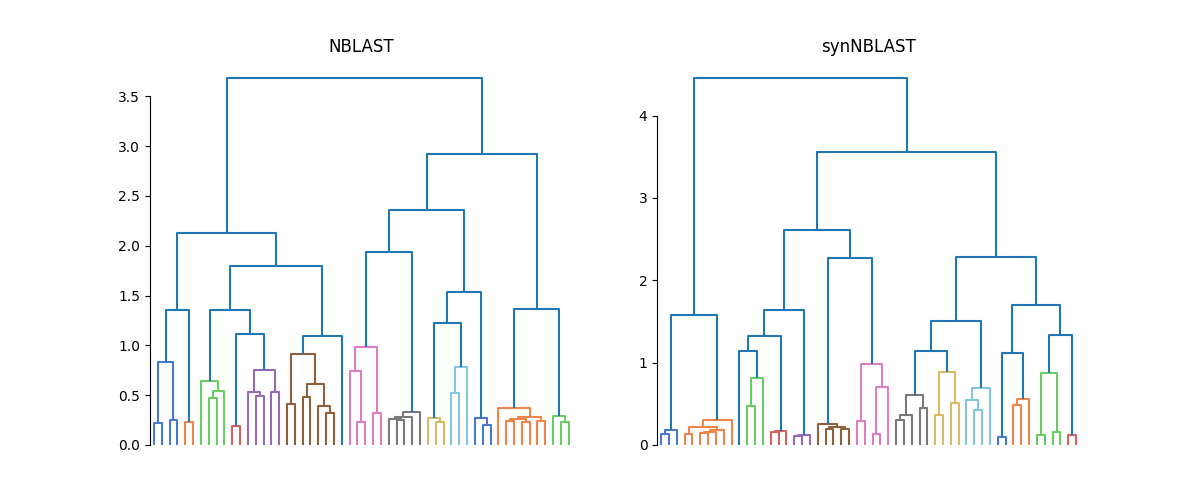
fig, axes = plt.subplots(1, 2, figsize=(12, 5))

dn1 = dendrogram(Z_nbl, no_labels=True, color_threshold=1, ax=axes[0])
dn2 = dendrogram(Z_synbl, no_labels=True, color_threshold=1, ax=axes[1])

axes[0].set_title("NBLAST")
axes[1].set_title("synNBLAST")

sns.despine(trim=True, bottom=True)

While we don't know which leaf is which, the structure in both dendrograms looks similar. If we wanted to take it further than that, we could use tanglegram to line up the two clusterings and compare them.

But let's save that for another day and instead do some plotting:

Generate clusters

from scipy.cluster.hierarchy import fcluster

cl = fcluster(Z_synbl, t=1, criterion="distance")
cl

Out:

array([ 6,  6, 14,  6,  8,  8,  3,  8,  2, 15,  2,  7,  8,  2, 13, 10, 10,
       14, 13,  1,  1,  3, 11, 10, 10,  2,  2,  7,  2,  7,  7,  7,  9,  9,
       11,  9,  4,  3,  5,  9,  9, 12, 14, 14, 11, 15, 12, 11, 13,  2,  5,
        5,  8,  1], dtype=int32)

Now plot each cluster. For simplicity we are plotting in 2D here:

import math

n_clusters = max(cl)
rows = 4
cols = math.ceil(n_clusters / 4)
fig, axes = plt.subplots(rows, cols, figsize=(20, 5 * cols))
# Flatten axes
axes = [ax for l in axes for ax in l]

# Generate colors
pal = sns.color_palette("muted", n_clusters)

for i in range(n_clusters):
    ax = axes[i]
    ax.set_title(f"cluster {i + 1}")
    # Get the neurons in this cluster
    this = pns[cl == (i + 1)]

    navis.plot2d(
        this, method="2d", ax=ax, color=pal[i], lw=1.5, view=("x", "-z"), alpha=0.5
    )

for ax in axes:
    ax.set_aspect("equal")
    ax.set_axis_off()

    # Set all axes to the same limits
    bbox = pns.bbox
    ax.set_xlim(bbox[0][0], bbox[0][1])
    ax.set_ylim(bbox[2][1], bbox[2][0])

plt.tight_layout()

Note how clusters 3 and 8 look a bit odd? That's because these likely still contain more than one type of neuron. We should probably have gone with a slightly finer clustering. But this little demo should be enough to get you started!

Total running time of the script: ( 0 minutes 59.800 seconds)

Download Python source code: tutorial_nblast_00_intro.py

Download Jupyter notebook: tutorial_nblast_00_intro.ipynb

Gallery generated by mkdocs-gallery